4. Grafos, Nodos y Relaciones.

Para representar la información de los vínculos que se entretejen entre los actores sociales, el análisis de redes sociales utiliza dos elementos tomados directamente de la matemática: matrices y grafos. Es de notar que los científicos sociales sólo utilizan algunas de las técnicas matemáticas aportadas por la teoría de grafos y el álgebra lineal, los cuales son en sí mismos campos amplísimos dentro de las ciencias.

Se conoce como socio-grama a las representaciones gráficas de las redes sociales, con la finalidad de distinguirlas de otros tipos de gráficos (histogramas, gráficos circulares, polígonos de frecuencias). Aunque existen ciertas variaciones dentro de la forma en que se representan las redes, todos los socio-gramas utilizan un vértice etiquetado para cada actor en la población descrita, así como segmentos de líneas entre dos actores para representar la existencia de un vínculo entre ellos. El Gráfico 1 presenta el socio-grama que se obtiene al graficar las relaciones mostradas por la Tabla II.

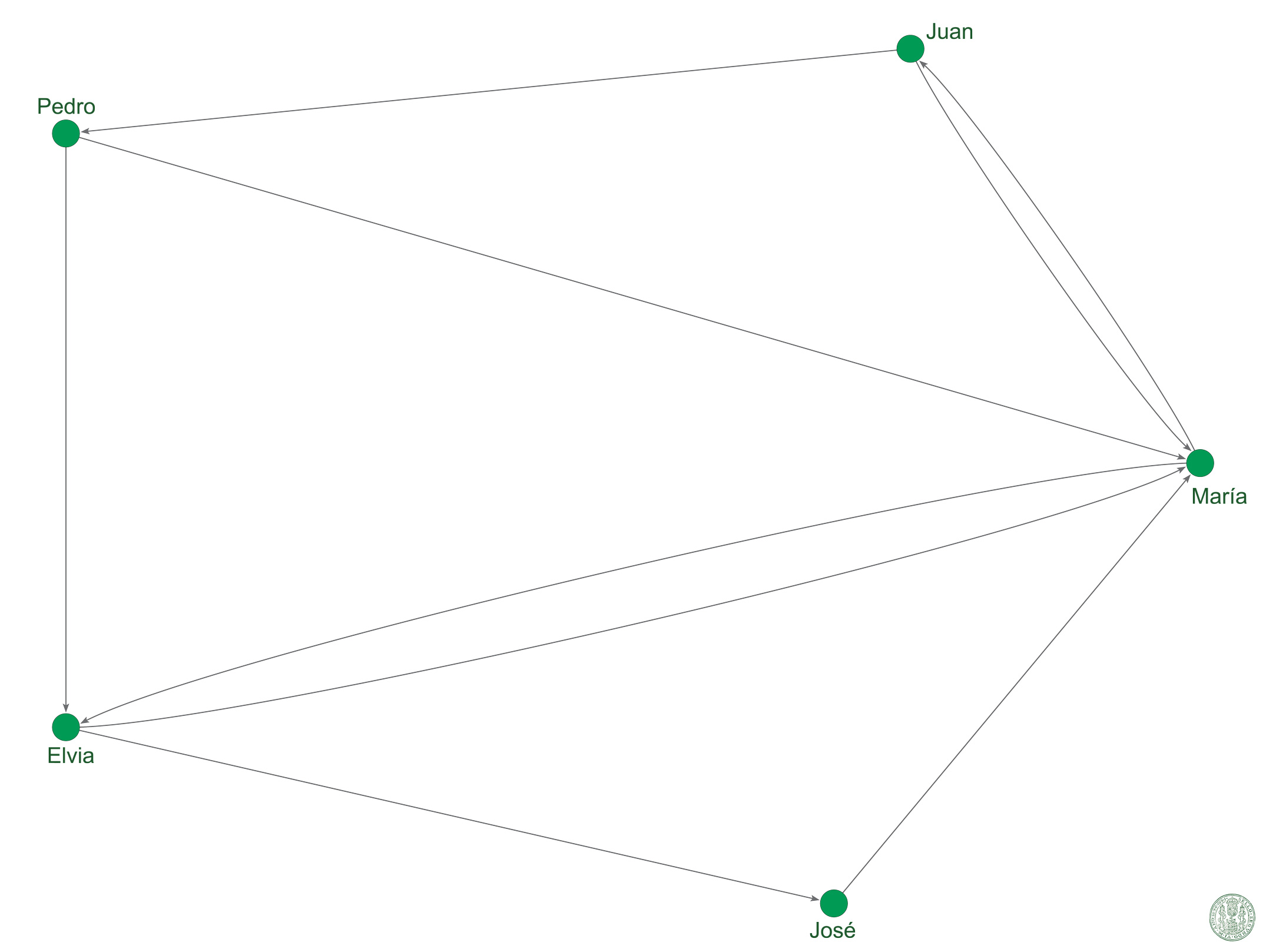
Gráfico 1: Socio-grama dibujado a partir de la Tabla II. 

Los datos de la red son definidos por los actores y sus relaciones. Comienzo por los actores de la red, es decir los nodos, que en el Gráfico 1 aparecen como círculos verdes. Estos actores pueden ser individuos, como en este caso, o bien instituciones, conceptos, y un largo etc. Para identificar a cada uno de los actores, en este caso, se utilizó una etiqueta con el nombre del personaje. Aunque este procedimiento es muy práctico, se debe decir que sólo se puede utilizar cuando los personajes analizados son pocos; el lienzo de la red se comienza a abigarrar de manera muy vertiginosa a partir de las pocas decenas de personajes. Existen, sin embargo, otras maneras de identificar a los actores: mediante colores, formas geométricas diferentes y el tamaño de los nodos.

Precisamente, las características intrínsecas de los actores pueden ser incorporadas como información adicional que permite identificar a los actores dentro del socio-grama. Por ejemplo, si conocemos el género de los participantes, podemos codificar los nodos mediante colores y formas. Para el caso del Gráfico 2, se puede observar la manera en que los nodos que representan a los hombres se han cambiado a cuadros verdes, mientras que los de las mujeres ahora son triángulos morados. Esto permite una identificación mucho más rápida de la información vertida en las Tablas I y II.

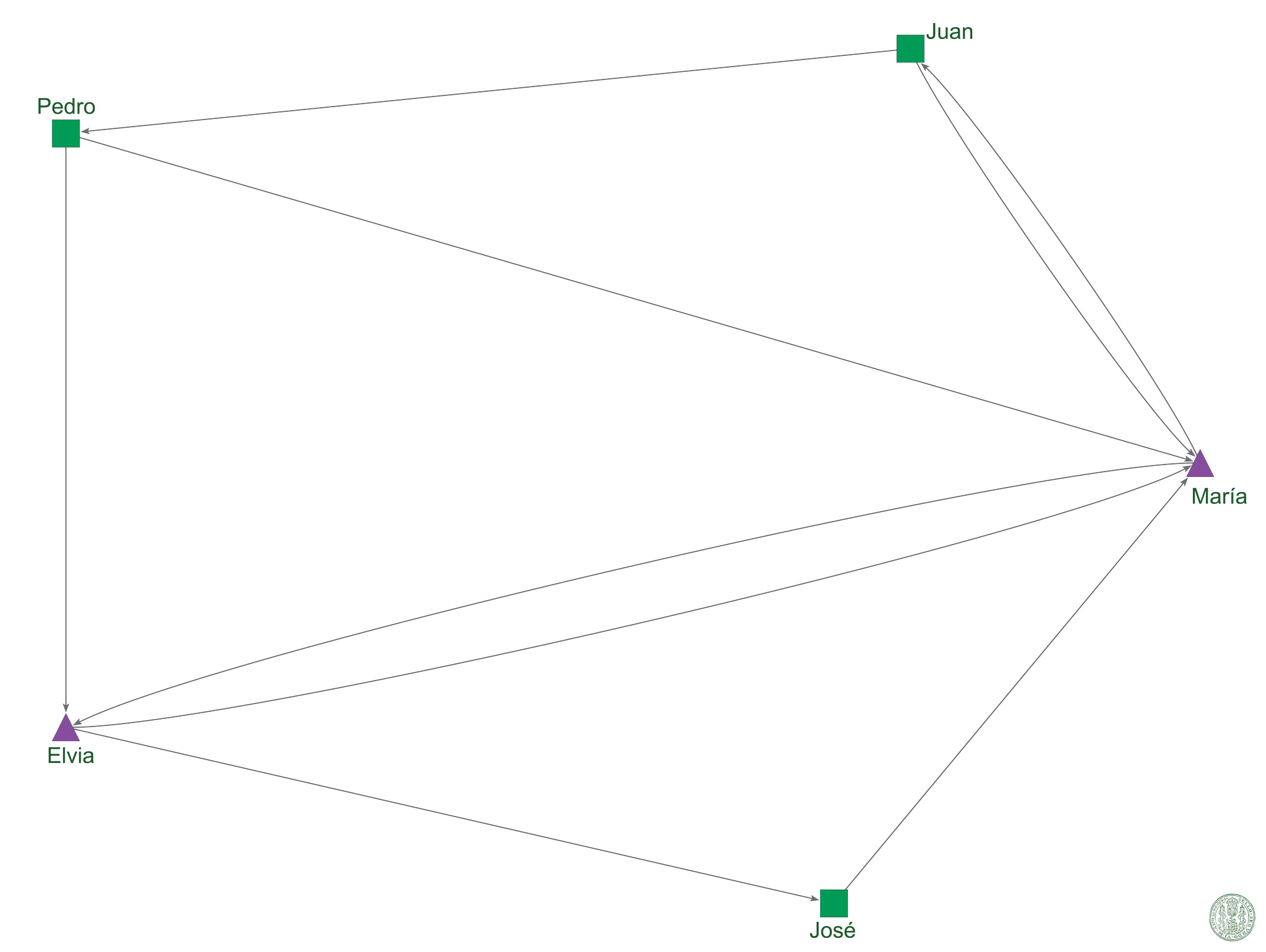
Gráfico 3: Socio-grama dibujado a partir de las Tablas I y II.

Para finalizar con los nodos, debe puntualizarse que el análisis de redes se interesa principalmente por las relaciones entre los actores de la red. Esto implica que los actores no son sopesados por sus características intrínsecas, como ocurre en otro tipo de estudios (notablemente las encuestas). Mientras la selección de los actores en estudios que no utilizan la teoría de redes tiende a darse mediante técnicas de muestreo estadístico, en A.R.S. se contemplan (inicialmente cuando menos) todos los actores existentes dentro de cierto límite.[1]

Una vez que he mencionado los principales elementos que componen a los nodos, abordo la otra mitad del análisis de redes sociales: las relaciones o vínculos. La problemática que plantean las relaciones entre nodos debe ser centrada, por principio de cuentas, en el tipo de información que se muestra mediante los vectores. El tipo de datos puede variar significativamente de acuerdo a la calidad de la información recabada, ya que existe un cierto tipo de muestreo en análisis de redes sociales. Además, se debe tener claro que el socio-grama y, por ende, el análisis de redes sociales, son un simple modelo de la realidad. Esto implica, necesariamente, una simplificación de la misma.

En términos generales, dentro de los grafos se presenta una sola relación. Pese a esto, se debe aclarar que para cualquier arreglo de actores puede existir un número n de relaciones que los vinculan; los sujetos sociales están inmersos en un mundo de relaciones familiares, económicas, intelectuales, religiosas, etc. Cuando se recaba información es común seleccionar sólo una o dos variables dentro de un grupo enorme de relaciones existentes, porque dichas relaciones son, cuando menos hipotéticamente, importantes a nivel estructural, ya que permiten analizar y describir el espacio social.

Existe una segunda problemática en torno a las relaciones entre nodos que se debe mencionar aquí: como muchos otros datos, la información recabada acerca de los vínculos entre actores puede ser medida. Las diferentes escalas de medida son importantes porque limitan el tipo de cuestiones que pueden ser examinadas por el investigador. También es importante tener una idea general acerca de las escalas de medida, ya que poseen diferentes propiedades matemáticas y por ende utilizan algoritmos diferentes al momento de describir patrones o probar inferencias sobre ellas.

La forma más común de medir relaciones es distinguirlas de la manera más simple: si existe vínculo, codificar la matriz con 1; si él vínculo no existe, se codifica con 0. A las redes así codificadas se les llama binarias. La matriz que se puede observar en la Tabla II es un ejemplo de red binaria. Se debe agregar que la mayoría de los algoritmos para medir las propiedades de los actores y redes han sido desarrollados para datos binarios. Es muy común que los datos medidos a un nivel superior deban ser transformados a sistema binario, para poder aplicar algún modelo analítico aportado por las matemáticas a la teoría de redes sociales. La pérdida de información es aceptable si el modelo a utilizar aporta una perspectiva nueva a la investigación.

En segundo término se encuentran las redes nominales. En este tipo de red, la escala utilizada es cualitativa: cada relación es codificada por su tipo. A diferencia de la escala binaria, una red nominal es de elección múltiple; se crean categorías codificadas para la información disponible. La forma más común para analizar valores nominales es usarlos para crear nuevas series de medidas binarias, de acuerdo a las posibilidades que los datos le permitan al investigador.

A veces es posible medir la fuerza de las relaciones de un actor mediante un rango ordenado de débil a fuerte. Las medidas ordinales pueden ser utilizadas para reflejar gran número de aspectos cuantitativos de las relaciones. Los analistas de redes se encuentran preocupados por describir la fuerza de las relaciones. El problema es que esa fuerza puede significar muchas cosas: frecuencia de la interacción, intensidad relacionada a un estado de ánimo, e incluso la existencia o ausencia de distintos tipos de vínculos. Es muy común que en las redes ordinales se tome en cuenta la reciprocidad de la relación, ya que esto supone la existencia de un vínculo que es compartido por los dos actores de la diada.

Finalmente, existen redes que se construyen a partir de datos continuos. Muchos de los datos que tienen que ver con actividad económica directa son continuos: intercambio de mercancías entre dos países medido en dólares, el P.I.B. de los países, etc. Es perfectamente posible construir matrices de A.R.S. incorporando estos datos. Existe, sin embargo, una gran limitación en la representación de gráfica de los mismos: el rango de valores que normalmente se obtiene a partir de los datos continuos es tan amplio, que termina siendo un tanto difícil de representar gráficamente.

Normalmente, la intensidad de los vínculos se representa alterando el ancho de las líneas que unen a los nodos, o bien agregando la información de su intensidad como etiquetas sobre las líneas. Ambas soluciones gráficas, sin embargo, son limitadas: para el caso de las etiquetas, en el momento en que existan muchas relaciones, es difícil saber a qué relación pertenece cada una de las etiquetas. Para el caso del grosor de las líneas la situación es mucho más compleja, pues para modificar el grueso, se deben utilizar medidas en puntos; una línea de 100 puntos amenaza muy rápidamente con ocupar todo el lienzo de nuestro grafo. Además, la varianza en los datos es difícil de representar de esta manera, pues muy difícil distinguir entre una línea con grosor de 35 puntos y otras con grosor de 36. Pese a todas estas indicaciones, debe quedar muy claro que el tipo de operaciones a nivel matricial que se pueden hacer con los datos continuos es muy completo, y existen muchos conceptos estructurales del A.R.S. que se pueden desarrollar. Precisamente, antes de concluir el presente artículo, me gustaría introducir un par de estos conceptos que permiten describir la red, analizarla y compararla con otras redes similares.