5. Densidad y Centralidad.
Una vez que se tiene vertida la matriz en el programa informático, además de generar un socio-grama para ser analizado visualmente, se pueden obtener una serie de coeficientes que permiten describir de manera general y particular la red. La mayoría de estos conceptos describen la estructura de las relaciones al interior de la red, y se puede intentar representar gráficamente esta información; en muchos de los programas sólo se necesita apretar un botón para convertir estos cálculos sobre la matriz en información gráfica sobre el socio – grama.
El primer concepto que me gustaría explorar es la densidad de la red, que muestra el recuento de los vínculos hacia otros actores de la red y los presenta como un ratio. Es útil para que el investigador conozca la cohesión de la red. La manera de calcular la densidad es muy simple: se cuentan las relaciones que ocurrieron en la matriz, y después se divide por el área total de la misma. Para el caso de la Tabla II, existen 9 vínculos en total entre los participantes, mientras que el área es de 25 (hay 5 participantes, luego entonces 5x5). Esto nos da una densidad de 0.36 o bien de 36% para toda la matriz. Pero en este caso en particular, la diagonal que se forma en la unión con el ego, es decir, la relación de María con María y de José con José no interesa, puesto que la pregunta original no admitía la respuesta “Elvia conoce a Elvia”. Luego entonces, para tener una densidad real debemos restar 5 al área total (el número de nuestros participantes). Haciendo esta operación, tenemos que la densidad sin bucles[1] es de 9/20, es decir, .45. A partir de estos sencillos coeficientes es posible describir la red que se tiene entre manos e, incluso, es posible compararla con otras redes. Por ejemplo, en este caso, se puede plantear la hipótesis de que el grupo estudiado tiene poca cohesión, puesto que la densidad de una red con tan pocos participantes normalmente tiende a 1.[2]
El siguiente concepto que expongo aquí es el de centralidad. En A.R.S., la centralidad muestra el papel y la posición de los actores en la red. Existen varias medidas que proporcionan un indicador del poder social de un nodo basándose en qué tan bien “conecta” dentro de la red. No me extenderé demasiado aquí, pues la centralidad es uno de los conceptos más estudiados por los analistas de redes sociales, y existe mucha información al respecto.[3] El primer coeficiente que se puede encontrar es el grado nodal. Esta es una medida de la cantidad de vectores que relacionan a un personaje con los demás nodos. Se puede interpretar como la oportunidad de influir o ser influido. El cálculo es muy sencillo: se suman, para cada nodo, los valores que aparecen en las columnas y en las filas asociadas a su nombre. El valor total es el grado nodal de ese personaje. Como ejemplo, para la matriz vertida en la Tabla II, se pueden encontrar los valores que he vertido en la Tabla III:
| Filas (Output) | Columnas (Input) | Grado Nodal | Porcentaje | |
| María | 2 | 4 | 6 | 33.33% |
| Juan | 2 | 1 | 3 | 16.67% |
| Pedro | 2 | 1 | 3 | 16.67% |
| Elvia | 2 | 2 | 4 | 22.22% |
| José | 1 | 1 | 2 | 11.11% |
Tabla III. Grado nodal a partir de la matriz en Tabla II.
En este ejemplo, se puede observar de manera muy simple que el personaje con más relaciones es María, pues hay seis líneas que la vinculan con cada uno de los otros personajes. Su grado nodal es de 6. También se puede expresar con un porcentaje, que se calcula de la siguiente manera: como ya se vio en la descripción de la densidad de la red, la cantidad total de relaciones en este ejemplo es de 9, pero como estamos contando estos vectores para cada uno de los nodos, el total es de 9 x 2 = 18. Ahora sólo tenemos que dividir el grado nodal entre 18 para obtener el porcentaje. En este sentido, la centralidad de María en la red es de 33%.
Ahora bien, gracias a la presentación de los datos en la Tabla III, es evidente que el grado nodal es una agregación de dos tipos de centralidad: las relaciones declaradas por los propios participantes, que se encuentra en las filas de la matriz (output), y las relaciones que los otros participantes declaran tener con el ego; estas relaciones aparecen en las columnas de la matriz (input). En el ejemplo vemos cómo las relaciones en las filas se distribuyen de manera parsimoniosa, pues cada uno de los personajes, salvo José, declaró conocer a dos personas dentro del grupo. Donde las cosas cambian es en las columnas, pues aquí todos los personajes declararon conocer a María, quien acumuló 4 menciones; la mayor cantidad que podía obtener. Esta distinción es útil para contrastar, en ciertos casos, la posición de los nodos respecto a su propia opinión dentro de la red (filas/output), y la que le asignan los demás participantes en la misma (columnas/input).
Además, es posible representar gráficamente los valores obtenidos mediante el cálculo de centralidad, con la finalidad de identificar de manera más fácil los nodos con mayor poder en la red. Como se puede observar en el Gráfico 3, el tamaño de los nodos ha sido alterado de acuerdo a la escala que nos muestra el grado nodal total; María es más grande que todos, pues es tocada por más líneas.
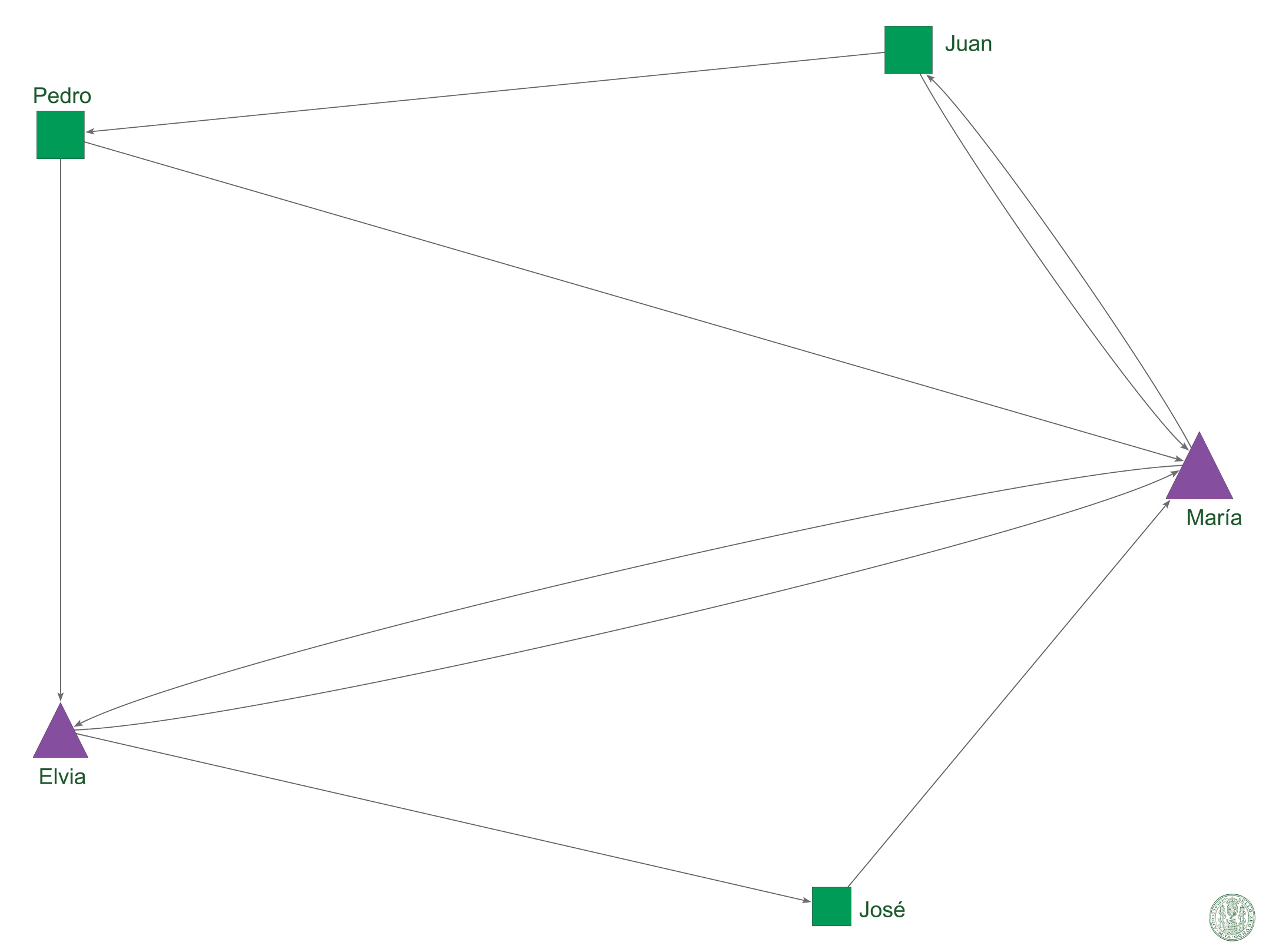
Gráfico 3: Socio-grama con valores de centralidad.
Este procedimiento es muy común: se crean nuevos valores a partir de conceptos del A.R.S. y se alimentan en el análisis para subrayar ciertas características, poniendo en relieve la manera en que se estructura la red. En este caso, la identificación del nodo con mayor centralidad. Ahora habrá que preguntarse el porqué de esta situación.
No me extenderé más sobre este punto porque el presente artículo es apenas una introducción al A.R.S.: acerca de la centralidad y cómo medirla hay gran cantidad de polémica. Sólo quiero dejar muy claro que la identificación de los nodos con centralidad, así como su posición en la red es una parte importante del A.R.S. También debo señalar que la densidad y la centralidad constituyen apenas el primer paso para iniciar la exploración de la red. Existen una serie de conceptos que son elaboraciones sobre estos elementos básicos, y que no desarrollaré aquí, tales como: clúster, rol, clasificación y brokerage.
[1] En los programas de A.R.S. a este grado de densidad se le llama normalmente “no loops allowed”.
[2] Una red con densidad = 1 o 100%, es también conocida como “red de mundo mínimo”, pues todos los participantes conocen a todos los participantes.



