Introducción al Análisis de Redes Sociales.
Resumen
El presente artículo explica algunos de los elementos básicos que estructuran el análisis de redes sociales, tales como sociograma, nodo, vector, relación, centralidad y densidad. Mediante una explicación sencilla, se pretende que los historiadores y otros humanistas conozcan los conceptos asociados al análisis de redes sociales, con la finalidad de que se acerquen a esta técnica. También se pone atención en la articulación entre la historia (y el problema de las fuentes documentales) y el A.R.S.
Palabras clave: Redes, Historia, Sociograma, Centralidad, Densidad
Abstract
This article explains some of the basic elements that structure the social network analysis. It defines concepts like sociogram, node, vector, relationship, centrality and density. The purpose is that historians and other scholars know the concepts associated to social network analysis, so that they can become familiar with the field. This is done through a clear and simple explanation. Finally, it explores the articulation of history with the problem of archival sources and social network analysis.
Key words: Networks, History, Sociogram, Centrality, Density.
1. Introducción.
En la última década, el Análisis de Redes Sociales (A.R.S.) se ha desarrollado como base de una creciente producción de investigaciones. La gran cantidad de publicaciones y revistas que se han escrito sobre este asunto es una muestra fehaciente de que el A.R.S. forma ya parte de las herramientas del investigador social.[1] Sin embargo, como en todo campo novedoso, la cantidad de información referente al tema hace un tanto difícil delimitar aquello que es mero ruido, de los elementos que componen la propuesta teórica subyacente. Precisamente por esto, el presente artículo presenta un acercamiento al Análisis de Redes Sociales.
Como señalaban Michel Bertrand, Sandro Guzzi y Claire Lemercier en el año 2011, en la disciplina histórica, la utilización del A.R.S. ha caminado por dos vías: aquellas investigaciones que se acercan de manera frontal a la formalización en términos técnicos que implica la aplicación del A.R.S., y aquellas que utilizan el concepto de red para explicar algún espacio de la realidad social, pero sin incorporar el análisis formal.[2] Es mi opinión que ambos acercamientos al campo de las redes sociales son plenamente válidos; la presentación de un socio-grama en el cuerpo de la investigación no garantiza que la elaboración del trabajo sea adecuada. De la misma manera, la ausencia de definiciones respecto a lo que es una red social, si este concepto es articulador de la investigación, puede dejar a ciertos trabajos en el limbo metodológico.
Creo que el problema de fondo es que estas dos maneras de acercarse al problema no dialogan lo suficiente, y que las dos perspectivas se podrían enriquecer mucho si se estableciese una comunicación entre los investigadores. En términos muy generales, parece que los investigadores que se inclinan por la presentación de modelos formales en los textos de A.R.S. provienen de disciplinas distintas a la historia (como la sociología o la antropología), mientras que los historiadores normalmente se inclinan por un acercamiento más laxo en términos metodológicos. Precisamente, el texto que se presenta a continuación, intenta explicar algunos conceptos básicos del análisis de redes sociales de una manera sencilla.
[1] Un buen termómetro para medir esta producción es la Revista Redes de la Universidad de Barcelona, que se encuentra en la siguiente dirección electrónica: http://revista-redes.rediris.es/ (consultado el 02/02/2015) Una pequeña vuelta por el sitio nos muestra que la cantidad de los trabajos es grande, así como sus temáticas: historia del arte, empresarial, sociología, economía, historia, etc.
[2] BERTRAND, M., GUZZI – HEBB, S. y LEMERCIER, C. (2011). Introducción: ¿en qué punto se encuentra el análisis de redes en Historia? Revista Redes, Volumen 21, p. 8.
2. Análisis de Redes Sociales.
La técnica conocida como Análisis de Redes Sociales, deriva de la disciplina sociológica, más específicamente de la sociometría propuesta por Jacob Levy Moreno[1], incorporando grandes préstamos de la teoría de grafos de la matemática de Frank Harary[2]. Se parte de una idea muy simple: los seres humanos,rankal interactuar entre sí, desarrollan diversos tipo de relaciones (p.ej. relaciones de parentesco o amistad, intercambios comerciales, etc.). Las relaciones sociales se asemejan a una red, porque conectan a los individuos.
Es preciso hacer notar que el supuesto teórico de esta forma de análisis, es que existen estructuras subyacentes en las todas las relaciones sociales. A diferencia (y tal vez en contraposición) de la sociología marxista, donde los individuos se encuentran subsumidos en relaciones de clase[3], esta propuesta pone el foco en las relaciones interpersonales. En el centro se encuentra el átomo social, que se compone del individuo y sus diversas relaciones; en A.R.S. se privilegia un acercamiento micro de la sociedad.
Parte central de esta interpretación de lo social es que la interacción de los individuos puede ser representada por un socio-grama. Es decir, un grafo que permite encontrar las características que estructuran la red de relaciones. Finalmente, la técnica de redes sociales propone una serie de procedimientos tomados de la estadística, para establecer el peso específico de cada una de las variables analizadas.
Aunque existen autores que proponen una teoría general de la historia a partir de los preceptos del A.R.S.[4], me encuentro convencido de que este enfoque constituye más bien una técnica de análisis. Ésta técnica es muy adecuada para cierto tipo de problemas, pero no para todos. Pienso que no se puede hablar de una “teoría de las redes” que permita subsumir toda la complejidad del mundo social a la idea de la estructura inmanente de una red. Esto, sin embargo, es un punto muy polémico y se debe poner atención a las diferentes posiciones que los autores exponen en los trabajos donde se aplica el A.R.S.[5]
[1] MORENO, J. L., (1941). Foundations of Sociometry: An Introduction. Sociometry, Volumen 4 (1), pp. 15 – 35.
[2] HARARY, Frank (1969). Graph Theory. E.U.A.: Addison – Wesley.
[3] KOHAN, Néstor (1998). Marx en su (Tercer) mundo. Buenos Aires: Biblos. Realiza una síntesis crítica del pensamiento marxista y de la noción de lucha de clases.
[4] McNEILL, J. R. & McNEILL, W. H. (2003). The human web. A bird’s – eye view of world history. E.U.A.: W. W. Norton & Company.
[5] En términos generales, la bibliografía sajona parece entender el Análisis de Redes Sociales como una teoría válida para dar explicaciones generales, como se puede desprender de los trabajos de los McNeil. Por otro lado, autores que se enmarcan dentro de la escuela franco-hispana agrupada en torno al proyecto FICHOZ, como Jose María Imizcoz y Jean Pierre Dedieu, aplican el concepto de red de manera más acotada en sus investigaciones. Ver: IMIZCOZ, J. M. (2004), Actores, redes, procesos: reflexiones para una historia más global. História. Revista de Facultade de Letras. Porto. III Série, Vol. 5, 2004, pp. 115 – 140.
3. Informática y Matrices.
La herramienta que se utiliza para ordenar la información de archivo en datos adecuados para aplicar modelos de A.R.S. es la computadora, a través de un software especializado.[1] Se debe mencionar que existen una gran cantidad de programas informáticos que permiten generar visualizaciones mediante la introducción de matrices relacionales. Empero, para las imágenes que se pueden encontrar en el presente artículo se utilizó Pajek.[2] Este programa se ha mantenido a lo largo de muchos años como estándar del A.R.S., permite realizar un gran número de operaciones sobre las matrices y tiene gran cantidad de cálculos bien definidos matemáticamente en su manual. También se debe apuntar que es un software que no demanda una computadora de última generación; los requerimientos de sistema son bastante racionales, llegando a funcionar en sistemas anticuados, pues su tamaño es reducido y puede ser instalado en sistemas con poca memoria (tanto en el disco duro como en RAM).[3] Aunque estas ventajas influyeron en la elección del software, debo aclarar que normalmente recomiendo su utilización por una razón mucho más simple: Pajek es un software libre.
También es preciso anotar que existen muchos buenos programas para generar visualizaciones de redes sociales, como Gephi, UCINET y VennMaker[4]. Es más, al ser más modernos en su concepción, creo que superan a Pajek en simplicidad de uso, pues su interfaz gráfica es más amable con el usuario final. Los dos últimos conllevan, sin embargo, un costo para ser instalados. Para finalizar este punto, se debe señalar que todos los programas aquí mencionados, junto con otros tantos que existen,[5] tienen sus ventajas y desventajas respecto a la utilización y resultados producidos. Al final del día, el escoger uno u otro se debe al gusto personal, así como a las limitaciones materiales que imponen las investigaciones.
Ahora bien, la información requerida para construir matrices de redes sociales (que posteriormente pueden ser transformadas en socio-gramas) no difiere mucho de ciertos datos estadísticos que son utilizados en la mayoría de las investigaciones. Estos datos, convencionalmente, consisten en arreglos de mediciones. El arreglo se representa mediante filas y columnas; las filas del arreglo son los casos, las columnas los atributos o variables. La Tabla I muestra un ejemplo de este tipo de arreglos:
| Nombre | Género | Edad |
| María | Mujer | 30 |
| Juan | Hombre | 28 |
| Pedro | Hombre | 45 |
| Elvia | Mujer | 25 |
| José | Hombre | 22 |
Tabla I. Ejemplo: Arreglo por columnas y filas (tabla de datos).
La finalidad de esta manera de representar los datos es que el arreglo muestre las semejanzas y diferencias de las variables en su distribución entre los casos. Los datos así organizados nos informan, por ejemplo, que María es una mujer de 30 años. En realidad, estamos describiendo las características intrínsecas de los personajes; sus atributos.
De la misma manera que estos datos ordenados en columnas y filas (tablas de datos), la información que se utiliza en A.R.S., en su forma más pura, consiste en un arreglo mediante columnas y filas. Las filas representan observaciones. Las columnas del arreglo representan el mismo grupo de observaciones. Cada celda del arreglo describe una relación entre los actores. La Tabla II presenta un ejemplo de la manera en que se organiza una matriz de datos relacionales:
| María | Juan | Pedro | Elvia | José | |
| María | --- | 1 | 0 | 1 | 0 |
| Juan | 1 | --- | 1 | 0 | 0 |
| Pedro | 1 | 0 | --- | 1 | 0 |
| Elvia | 1 | 0 | 0 | --- | 1 |
| José | 1 | 0 | 0 | 0 | --- |
Tabla II. Ejemplo. Matriz de una Red Social.
Para el caso de este pequeño ejemplo, a cada uno de los participantes en el arreglo se le pidió que declarase a quien conocía dentro del grupo. Hay sólo cinco personas en el grupo, los mismos que aparecen en la Tabla I. En caso de que existiese una relación declarada entre un par de participantes, se codificó con un número 1 en la intersección entre la columna y la fila que une a los nombres. Por el contrario, en caso de que no existiese una relación entre los personajes, se codificó con un número 0. Esta es una codificación booleana, porque utiliza sólo dos valores para saber si existe o no relación entre los participantes.
Se debe señalar que, para este caso, la pregunta que se realizó al grupo es a quién conocían dentro del mismo. La dirección del vínculo es importante aquí, pues en algunos casos, la relación no fue correspondida. Por ejemplo, Pedro afirmó conocer a María, pero ella no declaró conocerlo. Existen algunos casos en que al investigador le importa saber si las relaciones son en una vía o de ida y vuelta; otras veces, le importa únicamente que los personajes se relacionaron, sin importar la dirección de esta relación.
Como se puede ver, la lógica de las dos tablas es muy parecida: aunque se puede observar la información de la misma manera que en los datos con atributos (como en la Tabla I), el análisis de redes propone un cambio en la perspectiva: en lugar de centrarse en los actores y sus atributos, se pone énfasis en los actores y sus relaciones.
[1] La definición que se da del software de A.R.S. en: Social network analysis: Theory and applications “Social network analysis software is used to identify, represent, analyze, visualize, or simulate nodes (e.g. agents, organizations, or knowledge) and edges (relationships) from various types of input data (relational and non-relational), including mathematical models of social networks. The output data can be saved in external files. Various input and output file formats exist.” Este folleto es utilizado por la Universidad de Pennsilvania para los cursos sobre A.R.S: http://train.ed.psu.edu/WFED-543/SocNet_TheoryApp.pdf (consultado el 02/02/2015).
[2] Pajek puede ser descargado gratuitamente de la siguiente página: http://pajek.imfm.si/ (consultado el 02/02/2015). En este sitio también se puede encontrar información acerca de la correcta utilización del programa, y del A.R.S. en general.
[3] Tal vez su principal problema es que ha sido desarrollado sólo para el sistema operativo Windows. Sin embargo, mediante emuladores como Wine (que es también software libre), se puede utilizar en Mac OS X y también en algunas distribuciones de Linux. No hay, por el momento, aplicaciones que permitan su funcionamiento en sistemas operativos para plataformas móviles como Android o bien en iOS.
[4] El sitio de internet de UCINET es el siguiente: http://www.analytictech.com/ (consultado el 02/02/2015). Por su parte, VennMaker se puede encontrar en la siguiente liga: http://www.vennmaker.com/ (consultado el 02/02/2015).
[5] En Wikipedia se puede encontrar una lista muy práctica y actualizada periódicamente de los programas de A.R.S. existentes: http://en.wikipedia.org/wiki/Social_network_analysis_software (consultado el 02/02/2015).
4. Grafos, Nodos y Relaciones.
Para representar la información de los vínculos que se entretejen entre los actores sociales, el análisis de redes sociales utiliza dos elementos tomados directamente de la matemática: matrices y grafos. Es de notar que los científicos sociales sólo utilizan algunas de las técnicas matemáticas aportadas por la teoría de grafos y el álgebra lineal, los cuales son en sí mismos campos amplísimos dentro de las ciencias.
Se conoce como socio-grama a las representaciones gráficas de las redes sociales, con la finalidad de distinguirlas de otros tipos de gráficos (histogramas, gráficos circulares, polígonos de frecuencias). Aunque existen ciertas variaciones dentro de la forma en que se representan las redes, todos los socio-gramas utilizan un vértice etiquetado para cada actor en la población descrita, así como segmentos de líneas entre dos actores para representar la existencia de un vínculo entre ellos. El Gráfico 1 presenta el socio-grama que se obtiene al graficar las relaciones mostradas por la Tabla II.
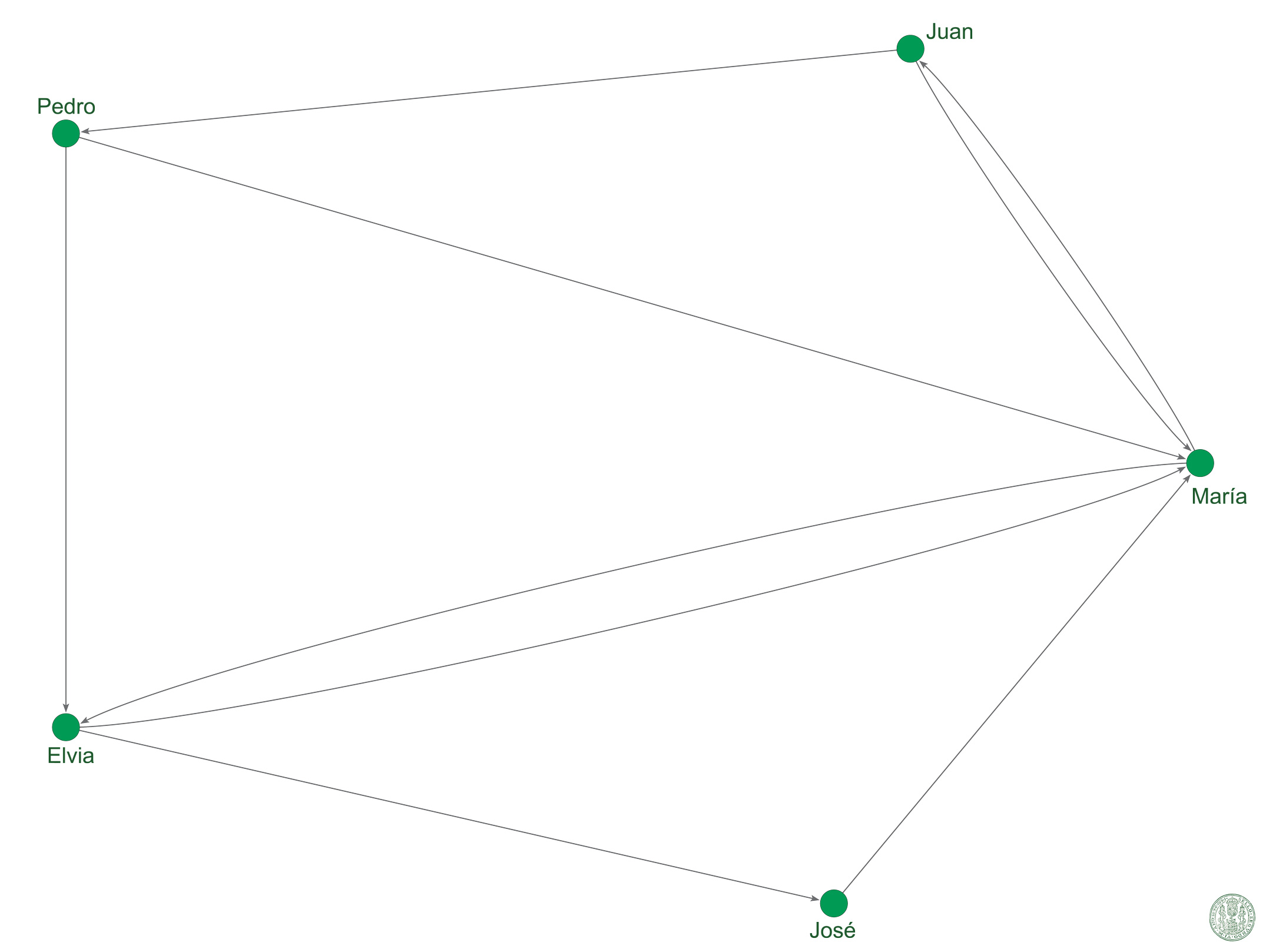
Gráfico 1: Socio-grama dibujado a partir de la Tabla II.
Los datos de la red son definidos por los actores y sus relaciones. Comienzo por los actores de la red, es decir los nodos, que en el Gráfico 1 aparecen como círculos verdes. Estos actores pueden ser individuos, como en este caso, o bien instituciones, conceptos, y un largo etc. Para identificar a cada uno de los actores, en este caso, se utilizó una etiqueta con el nombre del personaje. Aunque este procedimiento es muy práctico, se debe decir que sólo se puede utilizar cuando los personajes analizados son pocos; el lienzo de la red se comienza a abigarrar de manera muy vertiginosa a partir de las pocas decenas de personajes. Existen, sin embargo, otras maneras de identificar a los actores: mediante colores, formas geométricas diferentes y el tamaño de los nodos.
Precisamente, las características intrínsecas de los actores pueden ser incorporadas como información adicional que permite identificar a los actores dentro del socio-grama. Por ejemplo, si conocemos el género de los participantes, podemos codificar los nodos mediante colores y formas. Para el caso del Gráfico 2, se puede observar la manera en que los nodos que representan a los hombres se han cambiado a cuadros verdes, mientras que los de las mujeres ahora son triángulos morados. Esto permite una identificación mucho más rápida de la información vertida en las Tablas I y II.
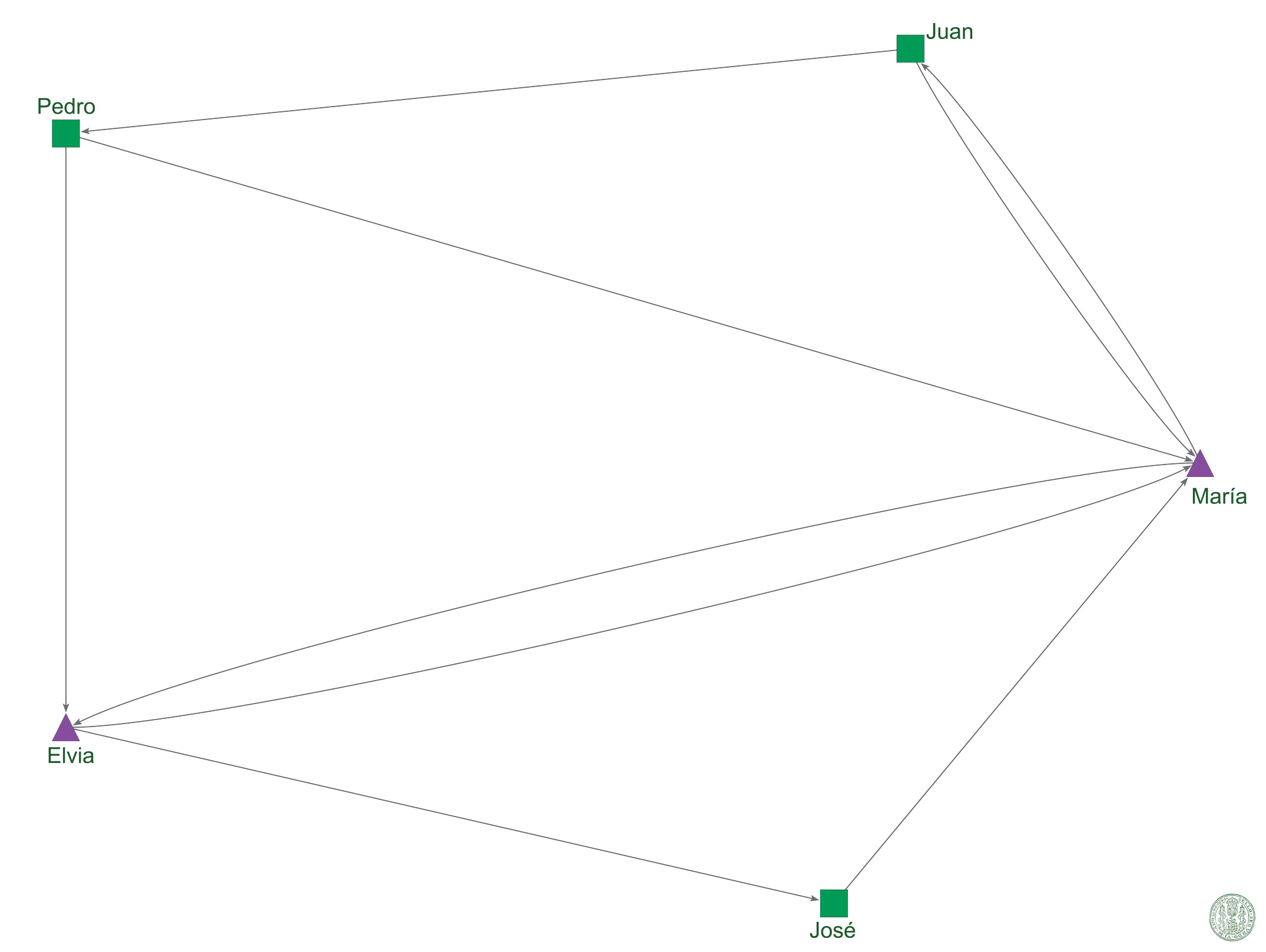
Gráfico 3: Socio-grama dibujado a partir de las Tablas I y II.
Para finalizar con los nodos, debe puntualizarse que el análisis de redes se interesa principalmente por las relaciones entre los actores de la red. Esto implica que los actores no son sopesados por sus características intrínsecas, como ocurre en otro tipo de estudios (notablemente las encuestas). Mientras la selección de los actores en estudios que no utilizan la teoría de redes tiende a darse mediante técnicas de muestreo estadístico, en A.R.S. se contemplan (inicialmente cuando menos) todos los actores existentes dentro de cierto límite.[1]
Una vez que he mencionado los principales elementos que componen a los nodos, abordo la otra mitad del análisis de redes sociales: las relaciones o vínculos. La problemática que plantean las relaciones entre nodos debe ser centrada, por principio de cuentas, en el tipo de información que se muestra mediante los vectores. El tipo de datos puede variar significativamente de acuerdo a la calidad de la información recabada, ya que existe un cierto tipo de muestreo en análisis de redes sociales. Además, se debe tener claro que el socio-grama y, por ende, el análisis de redes sociales, son un simple modelo de la realidad. Esto implica, necesariamente, una simplificación de la misma.
En términos generales, dentro de los grafos se presenta una sola relación. Pese a esto, se debe aclarar que para cualquier arreglo de actores puede existir un número n de relaciones que los vinculan; los sujetos sociales están inmersos en un mundo de relaciones familiares, económicas, intelectuales, religiosas, etc. Cuando se recaba información es común seleccionar sólo una o dos variables dentro de un grupo enorme de relaciones existentes, porque dichas relaciones son, cuando menos hipotéticamente, importantes a nivel estructural, ya que permiten analizar y describir el espacio social.
Existe una segunda problemática en torno a las relaciones entre nodos que se debe mencionar aquí: como muchos otros datos, la información recabada acerca de los vínculos entre actores puede ser medida. Las diferentes escalas de medida son importantes porque limitan el tipo de cuestiones que pueden ser examinadas por el investigador. También es importante tener una idea general acerca de las escalas de medida, ya que poseen diferentes propiedades matemáticas y por ende utilizan algoritmos diferentes al momento de describir patrones o probar inferencias sobre ellas.
La forma más común de medir relaciones es distinguirlas de la manera más simple: si existe vínculo, codificar la matriz con 1; si él vínculo no existe, se codifica con 0. A las redes así codificadas se les llama binarias. La matriz que se puede observar en la Tabla II es un ejemplo de red binaria. Se debe agregar que la mayoría de los algoritmos para medir las propiedades de los actores y redes han sido desarrollados para datos binarios. Es muy común que los datos medidos a un nivel superior deban ser transformados a sistema binario, para poder aplicar algún modelo analítico aportado por las matemáticas a la teoría de redes sociales. La pérdida de información es aceptable si el modelo a utilizar aporta una perspectiva nueva a la investigación.
En segundo término se encuentran las redes nominales. En este tipo de red, la escala utilizada es cualitativa: cada relación es codificada por su tipo. A diferencia de la escala binaria, una red nominal es de elección múltiple; se crean categorías codificadas para la información disponible. La forma más común para analizar valores nominales es usarlos para crear nuevas series de medidas binarias, de acuerdo a las posibilidades que los datos le permitan al investigador.
A veces es posible medir la fuerza de las relaciones de un actor mediante un rango ordenado de débil a fuerte. Las medidas ordinales pueden ser utilizadas para reflejar gran número de aspectos cuantitativos de las relaciones. Los analistas de redes se encuentran preocupados por describir la fuerza de las relaciones. El problema es que esa fuerza puede significar muchas cosas: frecuencia de la interacción, intensidad relacionada a un estado de ánimo, e incluso la existencia o ausencia de distintos tipos de vínculos. Es muy común que en las redes ordinales se tome en cuenta la reciprocidad de la relación, ya que esto supone la existencia de un vínculo que es compartido por los dos actores de la diada.
Finalmente, existen redes que se construyen a partir de datos continuos. Muchos de los datos que tienen que ver con actividad económica directa son continuos: intercambio de mercancías entre dos países medido en dólares, el P.I.B. de los países, etc. Es perfectamente posible construir matrices de A.R.S. incorporando estos datos. Existe, sin embargo, una gran limitación en la representación de gráfica de los mismos: el rango de valores que normalmente se obtiene a partir de los datos continuos es tan amplio, que termina siendo un tanto difícil de representar gráficamente.
Normalmente, la intensidad de los vínculos se representa alterando el ancho de las líneas que unen a los nodos, o bien agregando la información de su intensidad como etiquetas sobre las líneas. Ambas soluciones gráficas, sin embargo, son limitadas: para el caso de las etiquetas, en el momento en que existan muchas relaciones, es difícil saber a qué relación pertenece cada una de las etiquetas. Para el caso del grosor de las líneas la situación es mucho más compleja, pues para modificar el grueso, se deben utilizar medidas en puntos; una línea de 100 puntos amenaza muy rápidamente con ocupar todo el lienzo de nuestro grafo. Además, la varianza en los datos es difícil de representar de esta manera, pues muy difícil distinguir entre una línea con grosor de 35 puntos y otras con grosor de 36. Pese a todas estas indicaciones, debe quedar muy claro que el tipo de operaciones a nivel matricial que se pueden hacer con los datos continuos es muy completo, y existen muchos conceptos estructurales del A.R.S. que se pueden desarrollar. Precisamente, antes de concluir el presente artículo, me gustaría introducir un par de estos conceptos que permiten describir la red, analizarla y compararla con otras redes similares.
[1] No abordaré en este artículo las distintas maneras en que se puede abordar el muestreo de relaciones en A.R.S., porque se extendería muchísimo. Sólo mencionaré aquí que existen diversas estrategias para decidir cómo se llevará a cabo la recolección de información acerca de las relaciones entre nodos. El método de red total genera la mayor cantidad de información acerca de la estructura de la red, pero puede ser muy difícil de ejecutar ya que es costoso en tiempo y recursos. Por el otro lado, existen acercamientos que se parecen a los de muestreo simple, utilizado en cierto tipo de encuestas. Estos enfoques ofrecen menos información acerca de la estructura de la red, sin embargo son menos costosos y permiten una más fácil generalización de la información. Hay que puntualizar que no existe un modo correcto de búsqueda, y que las categorías generales deben ser adaptadas a la experiencia propia y las fuentes utilizadas en la investigación.
5. Densidad y Centralidad.
Una vez que se tiene vertida la matriz en el programa informático, además de generar un socio-grama para ser analizado visualmente, se pueden obtener una serie de coeficientes que permiten describir de manera general y particular la red. La mayoría de estos conceptos describen la estructura de las relaciones al interior de la red, y se puede intentar representar gráficamente esta información; en muchos de los programas sólo se necesita apretar un botón para convertir estos cálculos sobre la matriz en información gráfica sobre el socio – grama.
El primer concepto que me gustaría explorar es la densidad de la red, que muestra el recuento de los vínculos hacia otros actores de la red y los presenta como un ratio. Es útil para que el investigador conozca la cohesión de la red. La manera de calcular la densidad es muy simple: se cuentan las relaciones que ocurrieron en la matriz, y después se divide por el área total de la misma. Para el caso de la Tabla II, existen 9 vínculos en total entre los participantes, mientras que el área es de 25 (hay 5 participantes, luego entonces 5x5). Esto nos da una densidad de 0.36 o bien de 36% para toda la matriz. Pero en este caso en particular, la diagonal que se forma en la unión con el ego, es decir, la relación de María con María y de José con José no interesa, puesto que la pregunta original no admitía la respuesta “Elvia conoce a Elvia”. Luego entonces, para tener una densidad real debemos restar 5 al área total (el número de nuestros participantes). Haciendo esta operación, tenemos que la densidad sin bucles[1] es de 9/20, es decir, .45. A partir de estos sencillos coeficientes es posible describir la red que se tiene entre manos e, incluso, es posible compararla con otras redes. Por ejemplo, en este caso, se puede plantear la hipótesis de que el grupo estudiado tiene poca cohesión, puesto que la densidad de una red con tan pocos participantes normalmente tiende a 1.[2]
El siguiente concepto que expongo aquí es el de centralidad. En A.R.S., la centralidad muestra el papel y la posición de los actores en la red. Existen varias medidas que proporcionan un indicador del poder social de un nodo basándose en qué tan bien “conecta” dentro de la red. No me extenderé demasiado aquí, pues la centralidad es uno de los conceptos más estudiados por los analistas de redes sociales, y existe mucha información al respecto.[3] El primer coeficiente que se puede encontrar es el grado nodal. Esta es una medida de la cantidad de vectores que relacionan a un personaje con los demás nodos. Se puede interpretar como la oportunidad de influir o ser influido. El cálculo es muy sencillo: se suman, para cada nodo, los valores que aparecen en las columnas y en las filas asociadas a su nombre. El valor total es el grado nodal de ese personaje. Como ejemplo, para la matriz vertida en la Tabla II, se pueden encontrar los valores que he vertido en la Tabla III:
| Filas (Output) | Columnas (Input) | Grado Nodal | Porcentaje | |
| María | 2 | 4 | 6 | 33.33% |
| Juan | 2 | 1 | 3 | 16.67% |
| Pedro | 2 | 1 | 3 | 16.67% |
| Elvia | 2 | 2 | 4 | 22.22% |
| José | 1 | 1 | 2 | 11.11% |
Tabla III. Grado nodal a partir de la matriz en Tabla II.
En este ejemplo, se puede observar de manera muy simple que el personaje con más relaciones es María, pues hay seis líneas que la vinculan con cada uno de los otros personajes. Su grado nodal es de 6. También se puede expresar con un porcentaje, que se calcula de la siguiente manera: como ya se vio en la descripción de la densidad de la red, la cantidad total de relaciones en este ejemplo es de 9, pero como estamos contando estos vectores para cada uno de los nodos, el total es de 9 x 2 = 18. Ahora sólo tenemos que dividir el grado nodal entre 18 para obtener el porcentaje. En este sentido, la centralidad de María en la red es de 33%.
Ahora bien, gracias a la presentación de los datos en la Tabla III, es evidente que el grado nodal es una agregación de dos tipos de centralidad: las relaciones declaradas por los propios participantes, que se encuentra en las filas de la matriz (output), y las relaciones que los otros participantes declaran tener con el ego; estas relaciones aparecen en las columnas de la matriz (input). En el ejemplo vemos cómo las relaciones en las filas se distribuyen de manera parsimoniosa, pues cada uno de los personajes, salvo José, declaró conocer a dos personas dentro del grupo. Donde las cosas cambian es en las columnas, pues aquí todos los personajes declararon conocer a María, quien acumuló 4 menciones; la mayor cantidad que podía obtener. Esta distinción es útil para contrastar, en ciertos casos, la posición de los nodos respecto a su propia opinión dentro de la red (filas/output), y la que le asignan los demás participantes en la misma (columnas/input).
Además, es posible representar gráficamente los valores obtenidos mediante el cálculo de centralidad, con la finalidad de identificar de manera más fácil los nodos con mayor poder en la red. Como se puede observar en el Gráfico 3, el tamaño de los nodos ha sido alterado de acuerdo a la escala que nos muestra el grado nodal total; María es más grande que todos, pues es tocada por más líneas.
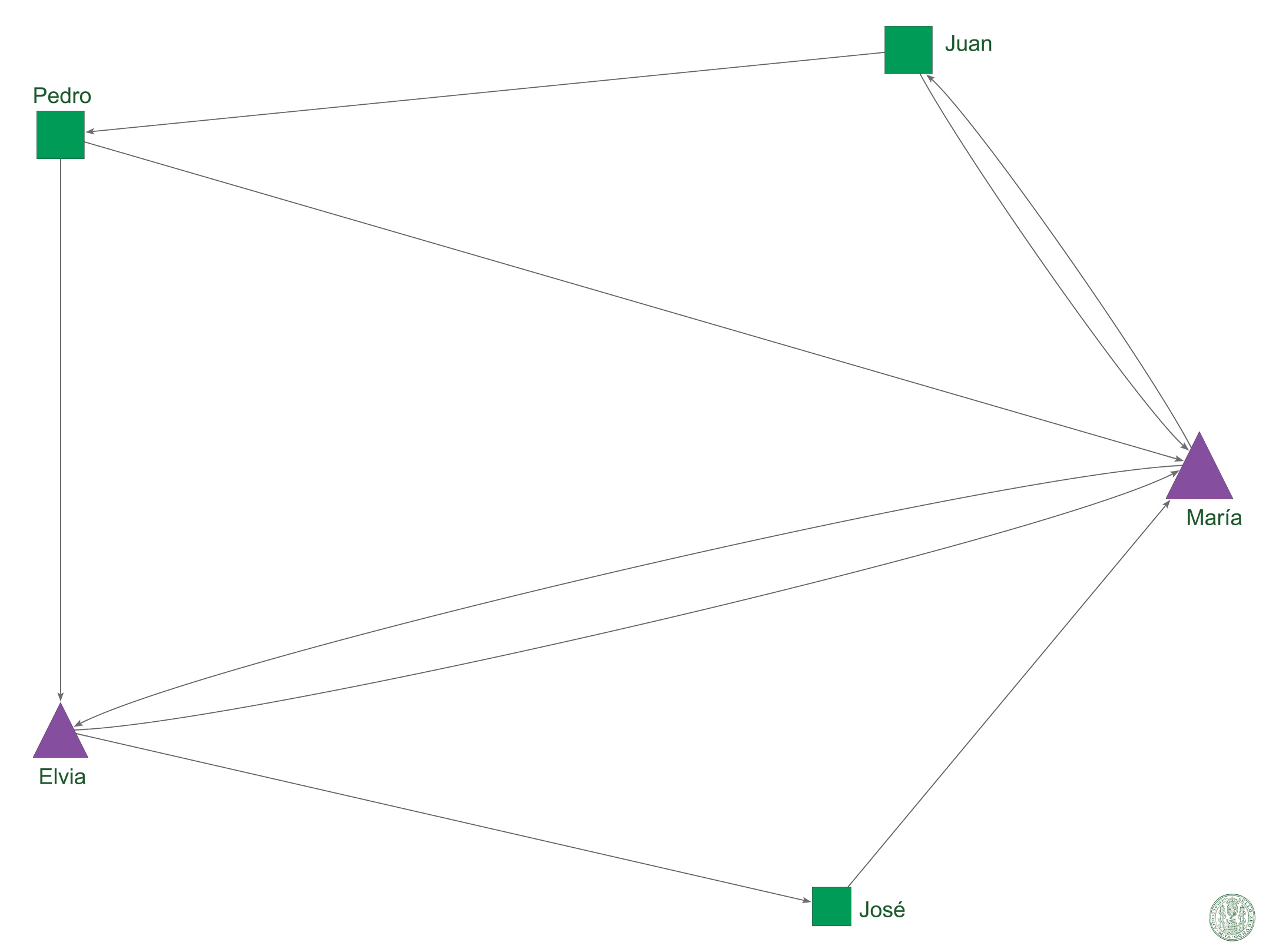
Gráfico 3: Socio-grama con valores de centralidad.
Este procedimiento es muy común: se crean nuevos valores a partir de conceptos del A.R.S. y se alimentan en el análisis para subrayar ciertas características, poniendo en relieve la manera en que se estructura la red. En este caso, la identificación del nodo con mayor centralidad. Ahora habrá que preguntarse el porqué de esta situación.
No me extenderé más sobre este punto porque el presente artículo es apenas una introducción al A.R.S.: acerca de la centralidad y cómo medirla hay gran cantidad de polémica. Sólo quiero dejar muy claro que la identificación de los nodos con centralidad, así como su posición en la red es una parte importante del A.R.S. También debo señalar que la densidad y la centralidad constituyen apenas el primer paso para iniciar la exploración de la red. Existen una serie de conceptos que son elaboraciones sobre estos elementos básicos, y que no desarrollaré aquí, tales como: clúster, rol, clasificación y brokerage.
[1] En los programas de A.R.S. a este grado de densidad se le llama normalmente “no loops allowed”.
[2] Una red con densidad = 1 o 100%, es también conocida como “red de mundo mínimo”, pues todos los participantes conocen a todos los participantes.
[3] Ver por ejemplo, las diversas definiciones de centralidad en el libro: NOOY DE, WOUTER, MRVAR, ANDREJ y BATAGELJ, VLADIMIR. (2005). Exploratory network analysis with Pajek. Nueva York: Cambridge University Press, pp. 242.
6. Conclusiones: la historia y el Análisis de Redes Sociales.
Parafraseando a Eric Van Young, creo que el análisis de redes sociales es “bueno para pensar” porque permite llamar la atención acerca de ciertas relaciones que, tal vez, no sean tan fáciles de apreciar a primera vista, sobre todo cuando se investigan grupos con un gran número de participantes.[1] También es un ejercicio que permite el diálogo entre enfoques de marcado corte cuantitativo y aquellas investigaciones que hacen de lo cualitativo su punto de partida; el modelo que se plantea por el A.R.S. es lo suficientemente laxo como para que se abarquen muchos tipos de investigaciones. Para aquellos que nos encontramos interesados por la historia económica, la propuesta es muy llamativa, pues permite el diálogo entre aquellos investigadores que gustan de los modelos y los que gustan más de la narratividad histórica.
Ahora bien, debo dejar muy claro que el trabajo de A.R.S. comienza, como todo tipo de investigación, con las fuentes. La investigación histórica tiene una fuerte carga empírica; sin información no existe la historia. El tratamiento de las fuentes es uno de los elementos centrales del trabajo histórico. A diferencia del sociólogo y el antropólogo, que trabajan con datos obtenidos a partir del trabajo de campo, y que pueden elaborar cuestionarios para aplicar a personas vivas, el historiador se enfrenta a sociedades del pasado que pudieron no haber dejado huellas documentales adecuadas para la aplicación del A.R.S. Sobre este punto, se debe decir que el tratamiento de las fuentes y su correcta interpretación, es un problema anterior a la decisión de cómo se van a utilizar analíticamente.
Una buena crítica de fuentes permite delimitar los problemas que se pueden tratar con la información disponible. El manejo y conocimiento profundo de las fuentes de primera mano, evita cometer el error de aplicar técnicas analíticas que requieren cierto tipo de datos que, a veces, no se ajustan al tipo de información que se puede obtener del archivo. Esto también implica que existen algunos temas que, sinceramente, se resisten a ser abordados mediante A.R.S. En términos generales, esta técnica modela mal las relaciones contradictorias en la sociedad: el rechazo, la pugna, la tensión, la guerra.[2] En contrapunto, hay una serie de temáticas que se prestan muy bien para ser tratadas mediante esta técnica, como el comercio, la migración, las relaciones de parentesco y compadrazgo, entre otros.
También es posible encontrar temáticas que son muy susceptibles para ser modeladas mediante A.R.S., pero que han dejado escasas huellas documentales de corte relacional, o bien dejaron repositorios de datos que no permiten una fácil modelización. En este punto, el investigador debe decidir si el plantear la temática mediante alguno de los conceptos estructurales de redes, aporta una mayor precisión analítica a su texto. Además, debo dejar anotada aquí la existencia de cierta polémica entre los historiadores que utilizan esta técnica: la modelética matemática es facultativa u obligatoria, es decir, ¿sin grafo no hay A.R.S?
No creo que el socio-grama sea tan importante, como para responder de manera categórica que el grafo hace al A.R.S. Es más, existen una gran cantidad de excelentes textos que aplican los conceptos estructurales de las redes sin utilizar el modelo matemático necesario para obtener socio-gramas.[3] Es mi opinión, sin embargo, que la modelización aportada por la teoría de grafos y el álgebra lineal es una de las partes más robustas del A.R.S., y que el investigador debería realizar el esfuerzo que implica ordenar los datos para obtener matrices relacionales y, posteriormente, socio-gramas. Este paso, cuando menos así lo creo, no es muy complicado de dar. Empero, la mayoría de las veces no se incursiona ahí por falta de información referente a la correcta sistematización de los datos. De acuerdo a mi experiencia en este campo, la mayoría de las veces sólo hace falta que el investigador organice su información, con la finalidad de ser leída por los programas informáticos que se encuentran disponibles para la generación del modelo. Espero que estos apuntes ayuden para que los historiadores intenten acercarse esta parte del A.R.S.
[1] VAN YOUNG, Eric. (1992). Mexico's Regions. Comparative History and Development. San Diego: University of California at San Diego., En la introducción a este libro el autor se pregunta si las regiones son “buenas para pensar”. Retomo la frase para aplicarla al A.R.S.
[2] Para una interesante crítica de estos límites: GARCÍA DE LEÓN, A. (2011). Tierra adentro, mar en fuera. El puerto de Veracruz y su litoral a Sotavento, 1519 – 1821. México: Fondo de Cultura Económica. pp. 501 – 535. En este apartado, García de León aborda la red de judíos portugueses que se encargaron de la introducción de esclavos en la primera mitad del siglo XVII en Veracruz, y muestra que el modelo del A.R.S. no pueda dar cuenta de toda la riqueza social; “El análisis de redes sociales (ARS), perfectamente aplicable a este caso particular, depsierta hoy muchas expectativas, y ello se debe en gran medida a la fascinación que ejercen los formalismos matemáticos en el relato de las ciencias sociales (en este caso, y tardíamente, entre los historiadores), independientemente de su utilidad o de su función heurística y olvidando que sólo es una aproximación intelectual amplia para identificar las estructuras sociales que emergen de las diversas formas de relación, pero sobre todo, un conjunto de métodos y técnicas.” Pp. 528.
[3] Ver, por ejemplo, el excelente trabajo de: ALCÁNTARA LÓPEZ, Á. (2007) Redes sociales, prácticas de poder y recomposición familiar en la provincia de Acayucan, 1784-1802. En VALLE PAVÓN DEL, G. e IBARRA, A. (Coordinadores.). Redes sociales e instituciones comerciales en el imperio español, siglos XVII a XIX. (pp. 215 - 248) México: Instituto Mora. En este texto se pone el foco de interés en una red del sotavento veracruzano que era económica, pero que no dejó las típicas huellas de corte económico, sino un sin fin de relaciones sociales que han sido reconstruidas por el autor de manera narrativa.
7. Bibliografía.
7.1 Libros.
- García de León Griego, Antonio Armando. (2011). Tierra adentro, mar en fuera. El puerto de Veracruz y su litoral a Sotavento, 1519 – 1821. México: Fondo de Cultura Económica.
- Harary, Frank. (1969). Graph Teory. E.U.A.: Addison - Wesley.
- Ibarra Romero, Antonio y Valle Pavón Del, Guillermina. (2007). Redes sociales e instituciones comerciales en el imperio español, siglos XVII a XIX. México: Instituto Mora.
- Kohan, Néstor. (1998). Marx en su (Tercer) mundo. Buenos Aires: Biblos.
- McNeill, J. R. y McNeill, W. H. (2003). The human web. A bird's - eye view of world history. E.U.A: Norton & Company.
- Nooy De, Wouter, Mrvar, Andrej y Batagelj, Vladimir. (2005). Exploratory network analisys with Pajek. Nueva York: Cambridge University Press.
- Van Young, Eric. (1992). Mexico's Regions. Comparative History and Development. San Diego: University of California at San Diego.
7.2 Revistas.
- Bertrand, M., Guzzi – Hebb, S. y Lemercier, C. (2011). Introducción: ¿en qué punto se encuentra el análisis de redes en Historia? Revista Redes, Volumen 21, pp. 1 – 12.
- Imízcoz José María (2004). Actores, redes, procesos: reflexiones para una historia más global. História. Revista de Facultade de Letras. Porto. III Série, Vol. 5, 2004, pp. 115 – 140.
- Moreno, J. L., (1941). Foundations of Sociometry: An Introduction. Sociometry, Volumen 4 (1), pp. 15 – 35.
7.3 Recursos electrónicos.
- http://revista-redes.rediris.es/ (consultado el 02/02/2015)
- http://pajek.imfm.si/ (consultado el 02/02/2015).
- http://www.analytictech.com/ (consultado el 02/02/2015).
- http://www.vennmaker.com/ (consultado el 02/02/2015).
- http://train.ed.psu.edu/WFED-543/SocNet_TheoryApp.pdf (consultado el 02/02/2015).
- http://en.wikipedia.org/wiki/Social_network_analysis_software (consultado el 02/02/2015).



